Time Series Forecasting Using Deep Learning

Load Data

Load the example data from WaveformData.mat. The data is a numObservations-by-1 cell array of sequences, where numObservations is the number of sequences. Each sequence is a numChannels-by-numTimeSteps numeric array, where numChannels is the number of channels of the sequence and numTimeSteps is the number of time steps of the sequence.

load WaveformData

View the sizes of the first few sequences.

data(1:5)

ans=5×1 cell array
    {3×103 double}
    {3×136 double}
    {3×140 double}
    {3×124 double}
    {3×127 double}

View the number of channels. To train the LSTM neural network, each sequence must have the same number of channels.

numChannels = size(data{1},1)

numChannels = 3

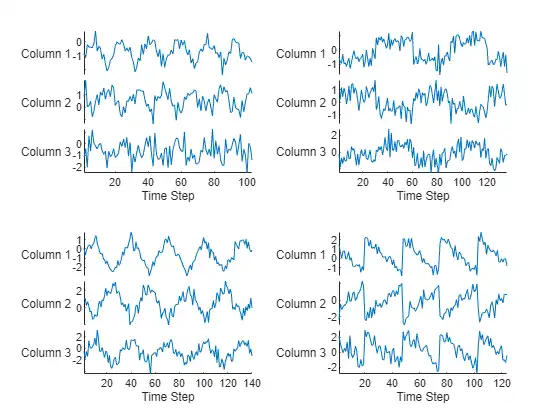
Visualize the first few sequences in a plot.

figure
tiledlayout(2,2)
for i = 1:4
    nexttile
    stackedplot(data{i}')

    xlabel("Time Step")
end

Partition the data into training and test sets. Use 90% of the observations for training and the remainder for testing.

numObservations = numel(data);
idxTrain = 1:floor(0.9*numObservations);
idxTest = floor(0.9*numObservations)+1:numObservations;
dataTrain = data(idxTrain);
dataTest = data(idxTest);

Prepare Data for Training

To forecast the values of future time steps of a sequence, specify the targets as the training sequences with values shifted by one time step. In other words, at each time step of the input sequence, the LSTM neural network learns to predict the value of the next time step. The predictors are the training sequences without the final time step.

for n = 1:numel(dataTrain)
    X = dataTrain{n};
    XTrain{n} = X(:,1:end-1);
    TTrain{n} = X(:,2:end);
end

For a better fit and to prevent the training from diverging, normalize the predictors and targets to have zero mean and unit variance. When you make predictions, you must also normalize the test data using the same statistics as the training data. To easily calculate the mean and standard deviation over all sequences, concatenate the sequences in the time dimension.

muX = mean(cat(2,XTrain{:}),2);
sigmaX = std(cat(2,XTrain{:}),0,2);

muT = mean(cat(2,TTrain{:}),2);
sigmaT = std(cat(2,TTrain{:}),0,2);

for n = 1:numel(XTrain)
    XTrain{n} = (XTrain{n} - muX) ./ sigmaX;
    TTrain{n} = (TTrain{n} - muT) ./ sigmaT;
end

Define LSTM Neural Network Architecture

Create an LSTM regression neural network.

layers = [
    sequenceInputLayer(numChannels)
    lstmLayer(128)
    fullyConnectedLayer(numChannels)
    regressionLayer];

Specify Training Options

Specify the training options.

options = trainingOptions("adam", ...
    MaxEpochs=200, ...
    SequencePaddingDirection="left", ...
    Shuffle="every-epoch", ...
    Plots="training-progress", ...
    Verbose=0);

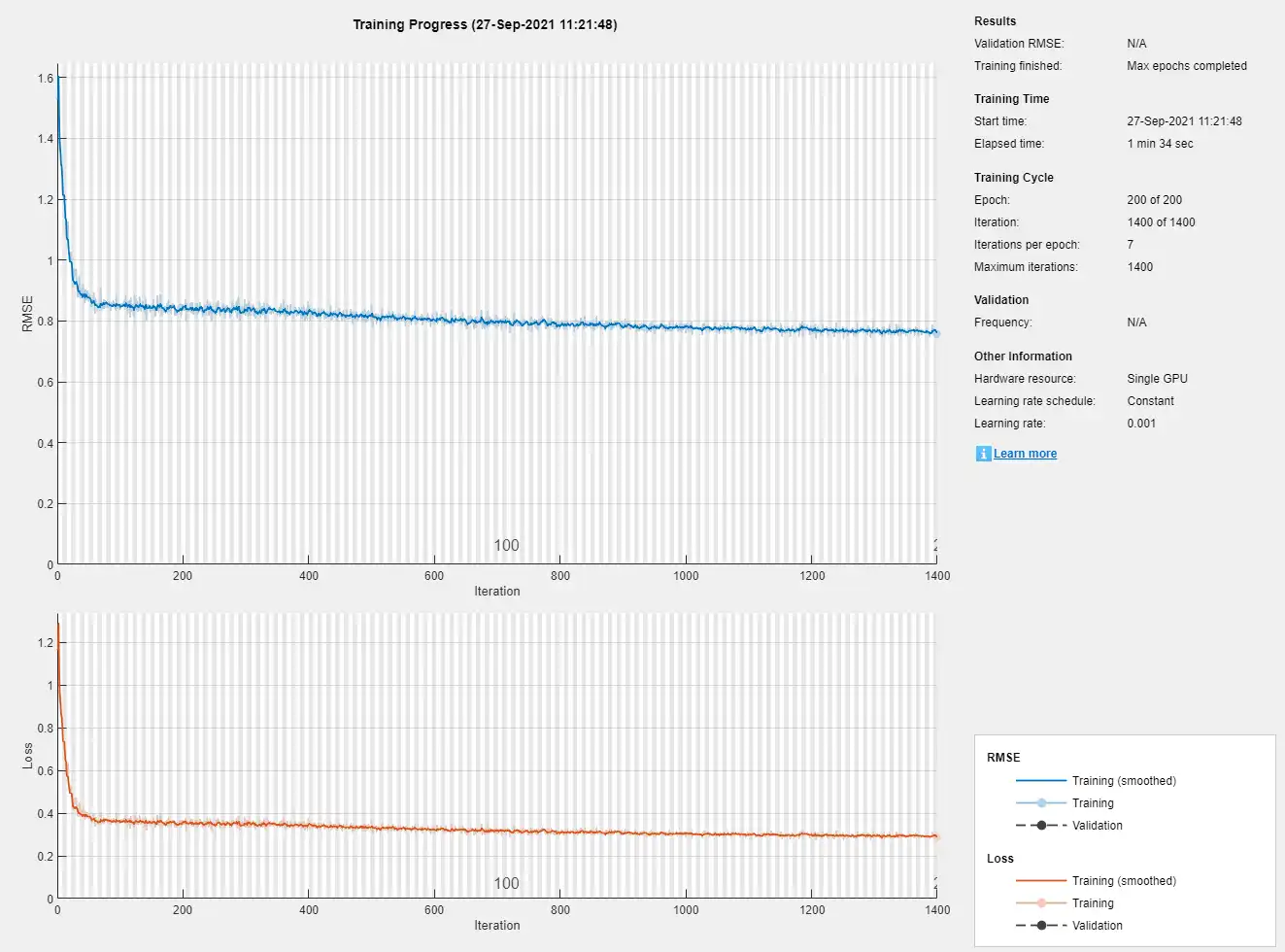
Train Recurrent Neural Network

Train the LSTM neural network with the specified training options using the trainNetwork function.

net = trainNetwork(XTrain,TTrain,layers,options);

Test Recurrent Neural Network

Prepare the test data for prediction using the same steps as for the training data.

Normalize the test data using the statistics calculated from the training data. Specify the targets as the test sequences with values shifted by one time step and the predictors as the test sequences without the final time step.

for n = 1:size(dataTest,1)
    X = dataTest{n};
    XTest{n} = (X(:,1:end-1) - muX) ./ sigmaX;
    TTest{n} = (X(:,2:end) - muT) ./ sigmaT;
end

Make predictions using the test data. Specify the same padding options as for training.

YTest = predict(net,XTest,SequencePaddingDirection="left");

To evaluate the accuracy, for each test sequence, calculate the root mean squared error (RMSE) between the predictions and the target.

for i = 1:size(YTest,1)
    rmse(i) = sqrt(mean((YTest{i} - TTest{i}).^2,"all"));
end

Visualize the errors in a histogram. Lower values indicate greater accuracy.

figure
histogram(rmse)
xlabel("RMSE")
ylabel("Frequency")

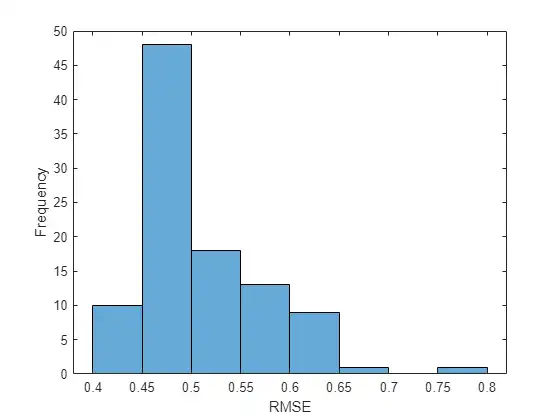
Calculate the mean RMSE over all test observations.

mean(rmse)

ans = single
    0.5080

Forecast Future Time Steps

Given an input time series or sequence, to forecast the values of multiple future time steps, use the predictAndUpdateState function to predict time steps one at a time and update the RNN state at each prediction. For each prediction, use the previous prediction as the input to the function.

Visualize one of the test sequences in a plot.

idx = 2;
X = XTest{idx};
T = TTest{idx};

figure
stackedplot(X',DisplayLabels="Channel " + (1:numChannels))
xlabel("Time Step")
title("Test Observation " + idx)

Open Loop Forecasting

Open loop forecasting predicts the next time step in a sequence using only the input data. When making predictions for subsequent time steps, you collect the true values from your data source and use those as input. For example, say you want to predict the value for time step t of a sequence using data collected in time steps 1 through t−1. To make predictions for time step t+1, wait until you record the true value for time step t and use that as input to make the next prediction. Use open loop forecasting when you have true values to provide to the RNN before making the next prediction.

Initialize the RNN state by first resetting the state using the resetState function, then make an initial prediction using the first few time steps of the input data. Update the RNN state using the first 75 time steps of the input data.

net = resetState(net);
offset = 75;
[net,~] = predictAndUpdateState(net,X(:,1:offset));

To forecast further predictions, loop over time steps and update the RNN state using the predictAndUpdateState function. Forecast values for the remaining time steps of the test observation by looping over the time steps of the input data and using them as input to the RNN. The first prediction is the value corresponding to the time step offset + 1.

numTimeSteps = size(X,2);
numPredictionTimeSteps = numTimeSteps - offset;
Y = zeros(numChannels,numPredictionTimeSteps);

for t = 1:numPredictionTimeSteps
    Xt = X(:,offset+t);
    [net,Y(:,t)] = predictAndUpdateState(net,Xt);
end

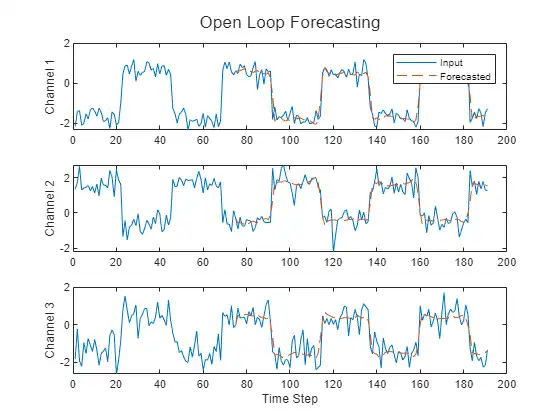
Compare the predictions with the target values.

figure
t = tiledlayout(numChannels,1);
title(t,"Open Loop Forecasting")

for i = 1:numChannels
    nexttile
    plot(T(i,:))
    hold on
    plot(offset:numTimeSteps,[T(i,offset) Y(i,:)],'--')
    ylabel("Channel " + i)
end

xlabel("Time Step")
nexttile(1)
legend(["Input" "Forecasted"])

Closed Loop Forecasting

Closed loop forecasting predicts subsequent time steps in a sequence by using the previous predictions as input. In this case, the model does not require the true values to make the prediction. For example, say you want to predict the value for time steps t through t+k of the sequence using data collected in time steps 1 through t−1 only. To make predictions for time step i, use the predicted value for time step i−1 as input. Use closed loop forecasting to forecast multiple subsequent time steps or when you do not have true values to provide to the RNN before making the next prediction.

Initialize the RNN state by first resetting the state using the resetState function, then make an initial prediction Z using the first few time steps of the input data. Update the RNN state using all time steps of the input data.

net = resetState(net);
offset = size(X,2);
[net,Z] = predictAndUpdateState(net,X);

To forecast further predictions, loop over time steps and update the RNN state using the predictAndUpdateState function. Forecast the next 200 time steps by iteratively passing the previous predicted value to the RNN. Because the RNN does not require the input data to make any further predictions, you can specify any number of time steps to forecast.

numPredictionTimeSteps = 200;
Xt = Z(:,end);
Y = zeros(numChannels,numPredictionTimeSteps);

for t = 1:numPredictionTimeSteps
    [net,Y(:,t)] = predictAndUpdateState(net,Xt);
    Xt = Y(:,t);
end

Visualize the forecasted values in a plot.

numTimeSteps = offset + numPredictionTimeSteps;

figure
t = tiledlayout(numChannels,1);
title(t,"Closed Loop Forecasting")

for i = 1:numChannels
    nexttile
    plot(T(i,1:offset))
    hold on
    plot(offset:numTimeSteps,[T(i,offset) Y(i,:)],'--')
    ylabel("Channel " + i)
end

xlabel("Time Step")
nexttile(1)
legend(["Input" "Forecasted"])

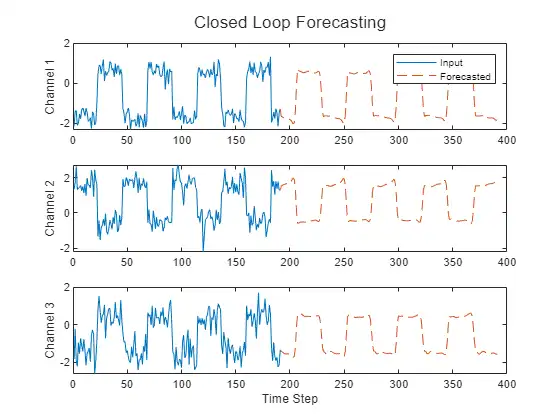
Closed loop forecasting allows you to forecast an arbitrary number of time steps, but can be less accurate when compared to open loop forecasting because the RNN does not have access to the true values during the forecasting process.