plotInteraction(mdl,'Cylinders','Weight','predictions')

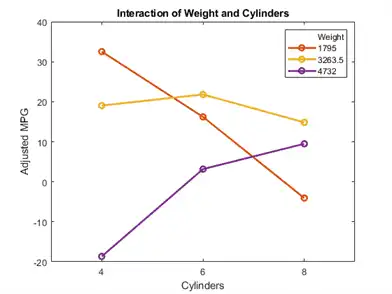
Now look at the interactions with various fixed levels of weight.
plotInteraction(mdl,'Weight','Cylinders','predictions')
Plots to Understand Terms Effects
This example shows how to understand the effect of each term in a regression model using a variety of available plots.
Create an added variable plot with Weight^2 as the added variable.
plotAdded(mdl,'Weight^2')
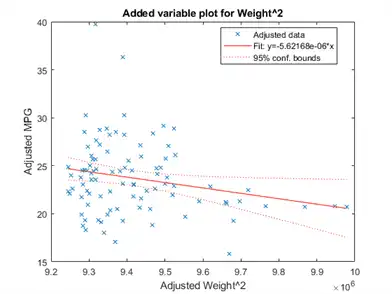
This plot shows the results of fitting both Weight^2 and MPG to the terms other than Weight^2. The reason to use plotAdded is to understand what additional improvement in the model you get by adding Weight^2. The coefficient of a line fit to these points is the coefficient of Weight^2 in the full model. The Weight^2 predictor is just over the edge of significance (pValue < 0.05) as you can see in the coefficients table display. You can see that in the plot as well. The confidence bounds look like they could not contain a horizontal line (constant y), so a zero-slope model is not consistent with the data.
Create an added variable plot for the model as a whole.
plotAdded(mdl)
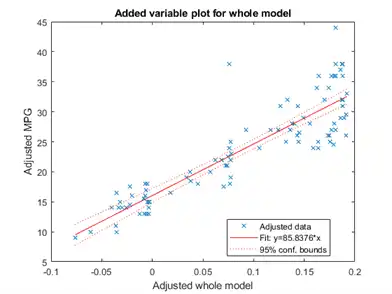
The model as a whole is very significant, so the bounds don't come close to containing a horizontal line. The slope of the line is the slope of a fit to the predictors projected onto their best-fitting direction, or in other words, the norm of the coefficient vector.
Change Models
There are two ways to change a model:
-
step— Add or subtract terms one at a time, wherestepchooses the most important term to add or remove. -
addTermsandremoveTerms— Add or remove specified terms. Give the terms in any of the forms described in Choose a Model or Range of Models.
If you created a model using stepwiselm, then step can have an effect only if you give different upper or lower models. step does not work when you fit a model using RobustOpts.
For example, start with a linear model of mileage from the carbig data:
load carbig tbl = table(Acceleration,Displacement,Horsepower,Weight,MPG); mdl = fitlm(tbl,'linear','ResponseVar','MPG')
mdl =
Linear regression model:
MPG ~ 1 + Acceleration + Displacement + Horsepower + Weight
Estimated Coefficients:
Estimate SE tStat pValue
__________ __________ ________ __________
(Intercept) 45.251 2.456 18.424 7.0721e-55
Acceleration -0.023148 0.1256 -0.1843 0.85388
Displacement -0.0060009 0.0067093 -0.89441 0.37166
Horsepower -0.043608 0.016573 -2.6312 0.008849
Weight -0.0052805 0.00081085 -6.5123 2.3025e-10
Number of observations: 392, Error degrees of freedom: 387
Root Mean Squared Error: 4.25
R-squared: 0.707, Adjusted R-Squared: 0.704
F-statistic vs. constant model: 233, p-value = 9.63e-102
Try to improve the model using step for up to 10 steps:
mdl1 = step(mdl,'NSteps',10)
1. Adding Displacement:Horsepower, FStat = 87.4802, pValue = 7.05273e-19
mdl1 =
Linear regression model:
MPG ~ 1 + Acceleration + Weight + Displacement*Horsepower
Estimated Coefficients:
Estimate SE tStat pValue
__________ __________ _______ __________
(Intercept) 61.285 2.8052 21.847 1.8593e-69
Acceleration -0.34401 0.11862 -2.9 0.0039445
Displacement -0.081198 0.010071 -8.0623 9.5014e-15
Horsepower -0.24313 0.026068 -9.3265 8.6556e-19
Weight -0.0014367 0.00084041 -1.7095 0.088166
Displacement:Horsepower 0.00054236 5.7987e-05 9.3531 7.0527e-19
Number of observations: 392, Error degrees of freedom: 386
Root Mean Squared Error: 3.84
R-squared: 0.761, Adjusted R-Squared: 0.758
F-statistic vs. constant model: 246, p-value = 1.32e-117
step stopped after just one change.
To try to simplify the model, remove the Acceleration and Weight terms from mdl1:
mdl2 = removeTerms(mdl1,'Acceleration + Weight')
mdl2 =
Linear regression model:
MPG ~ 1 + Displacement*Horsepower
Estimated Coefficients:
Estimate SE tStat pValue
__________ _________ _______ ___________
(Intercept) 53.051 1.526 34.765 3.0201e-121
Displacement -0.098046 0.0066817 -14.674 4.3203e-39
Horsepower -0.23434 0.019593 -11.96 2.8024e-28
Displacement:Horsepower 0.00058278 5.193e-05 11.222 1.6816e-25
Number of observations: 392, Error degrees of freedom: 388
Root Mean Squared Error: 3.94
R-squared: 0.747, Adjusted R-Squared: 0.745
F-statistic vs. constant model: 381, p-value = 3e-115
mdl2 uses just Displacement and Horsepower, and has nearly as good a fit to the data as mdl1 in the Adjusted R-Squared metric.
Predict or Simulate Responses to New Data
A LinearModel object offers three functions to predict or simulate the response to new data: predict, feval, and random.
predict
Use the predict function to predict and obtain confidence intervals on the predictions.
Load the carbig data and create a default linear model of the response MPG to the Acceleration, Displacement, Horsepower, and Weight predictors.
load carbig X = [Acceleration,Displacement,Horsepower,Weight]; mdl = fitlm(X,MPG);
Create a three-row array of predictors from the minimal, mean, and maximal values. X contains some NaN values, so specify the 'omitnan' option for the mean function. The min and max functions omit NaN values in the calculation by default.
Xnew = [min(X);mean(X,'omitnan');max(X)];
Find the predicted model responses and confidence intervals on the predictions.
[NewMPG, NewMPGCI] = predict(mdl,Xnew)
NewMPG = 3×1
34.1345
23.4078
4.7751
NewMPGCI = 3×2
31.6115 36.6575
22.9859 23.8298
0.6134 8.9367
The confidence bound on the mean response is narrower than those for the minimum or maximum responses.
feval
Use the feval function to predict responses. When you create a model from a table or dataset array, feval is often more convenient than predict for predicting responses. When you have new predictor data, you can pass it to feval without creating a table or matrix. However, feval does not provide confidence bounds.
Load the carbig data set and create a default linear model of the response MPG to the predictors Acceleration, Displacement, Horsepower, and Weight.
load carbig tbl = table(Acceleration,Displacement,Horsepower,Weight,MPG); mdl = fitlm(tbl,'linear','ResponseVar','MPG');
Predict the model response for the mean values of the predictors.
NewMPG = feval(mdl,mean(Acceleration,'omitnan'),mean(Displacement,'omitnan'),mean(Horsepower,'omitnan'),mean(Weight,'omitnan'))
NewMPG = 23.4078
random
Use the random function to simulate responses. The random function simulates new random response values, equal to the mean prediction plus a random disturbance with the same variance as the training data.
Load the carbig data and create a default linear model of the response MPG to the Acceleration, Displacement, Horsepower, and Weight predictors.
load carbig X = [Acceleration,Displacement,Horsepower,Weight]; mdl = fitlm(X,MPG);
Create a three-row array of predictors from the minimal, mean, and maximal values.
Xnew = [min(X);mean(X,'omitnan');max(X)];
Generate new predicted model responses including some randomness.
rng('default') % for reproducibility
NewMPG = random(mdl,Xnew)
NewMPG = 3×1
36.4178
31.1958
-4.8176
Because a negative value of MPG does not seem sensible, try predicting two more times.
NewMPG = random(mdl,Xnew)
NewMPG = 3×1
37.7959
24.7615
-0.7783
NewMPG = random(mdl,Xnew)
NewMPG = 3×1
32.2931
24.8628
19.9715
Clearly, the predictions for the third (maximal) row of Xnew are not reliable.
Share Fitted Models
Suppose you have a linear regression model, such as mdl from the following commands.
load carbig tbl = table(Acceleration,Displacement,Horsepower,Weight,MPG); mdl = fitlm(tbl,'linear','ResponseVar','MPG');
To share the model with other people, you can:
-
Provide the model display.
mdl
mdl =
Linear regression model:
MPG ~ 1 + Acceleration + Displacement + Horsepower + Weight
Estimated Coefficients:
Estimate SE tStat pValue
__________ __________ ________ __________
(Intercept) 45.251 2.456 18.424 7.0721e-55
Acceleration -0.023148 0.1256 -0.1843 0.85388
Displacement -0.0060009 0.0067093 -0.89441 0.37166
Horsepower -0.043608 0.016573 -2.6312 0.008849
Weight -0.0052805 0.00081085 -6.5123 2.3025e-10
Number of observations: 392, Error degrees of freedom: 387
Root Mean Squared Error: 4.25
R-squared: 0.707, Adjusted R-Squared: 0.704
F-statistic vs. constant model: 233, p-value = 9.63e-102
-
Provide the model definition and coefficients.
mdl.Formula
ans = MPG ~ 1 + Acceleration + Displacement + Horsepower + Weight
mdl.CoefficientNames
ans = 1x5 cell
Columns 1 through 4
{'(Intercept)'} {'Acceleration'} {'Displacement'} {'Horsepower'}
Column 5
{'Weight'}
mdl.Coefficients.Estimate
ans = 5×1
45.2511
-0.0231
-0.0060
-0.0436
-0.0053