Examine Quality and Adjust the Fitted Nonlinear Model
There are diagnostic plots to help you examine the quality of a model. plotDiagnostics(mdl) gives a variety of plots, including leverage and Cook's distance plots. plotResiduals(mdl) gives the difference between the fitted model and the data.
There are also properties of mdl that relate to the model quality. mdl.RMSE gives the root mean square error between the data and the fitted model. mdl.Residuals.Raw gives the raw residuals. mdl.Diagnostics contains several fields, such as Leverage and CooksDistance, that can help you identify particularly interesting observations.
This example shows how to examine a fitted nonlinear model using diagnostic, residual, and slice plots.
Load the sample data.
load reaction
Create a nonlinear model of rate as a function of reactants using the hougen.m function.
beta0 = ones(5,1);
mdl = fitnlm(reactants,...
rate,@hougen,beta0);
Make a leverage plot of the data and model.
plotDiagnostics(mdl)
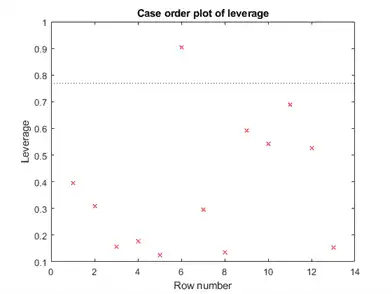
There is one point that has high leverage. Locate the point.
[~,maxl] = max(mdl.Diagnostics.Leverage)
maxl = 6
Examine a residuals plot.
plotResiduals(mdl,'fitted')
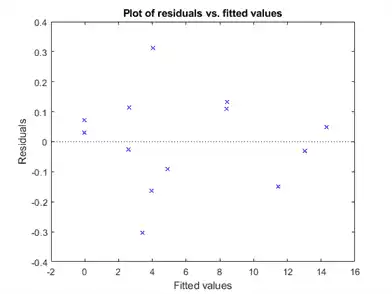
Nothing stands out as an outlier.
Use a slice plot to show the effect of each predictor on the model.
plotSlice(mdl)
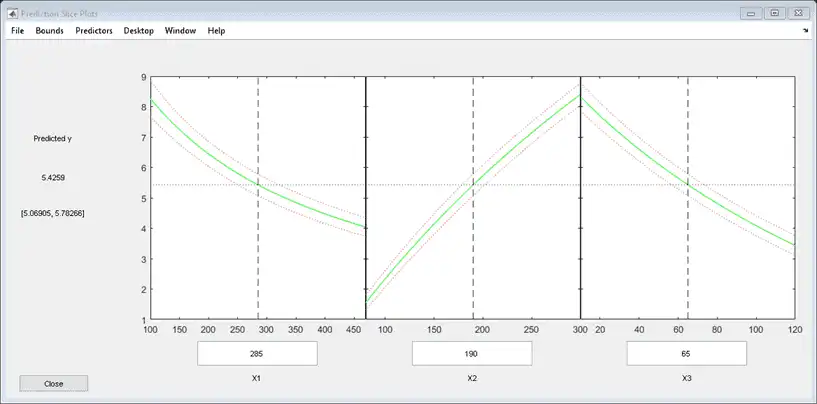
You can drag the vertical dashed blue lines to see the effect of a change in one predictor on the response. For example, drag the X2 line to the right, and notice that the slope of the X3 line changes.
Predict or Simulate Responses Using a Nonlinear Model
This example shows how to use the methods predict, feval, and random to predict and simulate responses to new data.
Randomly generate a sample from a Cauchy distribution.
rng('default')
X = rand(100,1);
X = tan(pi*X - pi/2);
Generate the response according to the model y = b1*(pi /2 + atan((x - b2) / b3)) and add noise to the response.
modelfun = @(b,x) b(1) * ...
(pi/2 + atan((x - b(2))/b(3)));
y = modelfun([12 5 10],X) + randn(100,1);
Fit a model starting from the arbitrary parameters b = [1,1,1].
beta0 = [1 1 1]; % An arbitrary guess mdl = fitnlm(X,y,modelfun,beta0)
mdl =
Nonlinear regression model:
y ~ b1*(pi/2 + atan((x - b2)/b3))
Estimated Coefficients:
Estimate SE tStat pValue
________ _______ ______ __________
b1 12.082 0.80028 15.097 3.3151e-27
b2 5.0603 1.0825 4.6747 9.5063e-06
b3 9.64 0.46499 20.732 2.0382e-37
Number of observations: 100, Error degrees of freedom: 97
Root Mean Squared Error: 1.02
R-Squared: 0.92, Adjusted R-Squared 0.918
F-statistic vs. zero model: 6.45e+03, p-value = 1.72e-111
The fitted values are within a few percent of the parameters [12,5,10].
Examine the fit.
plotSlice(mdl)
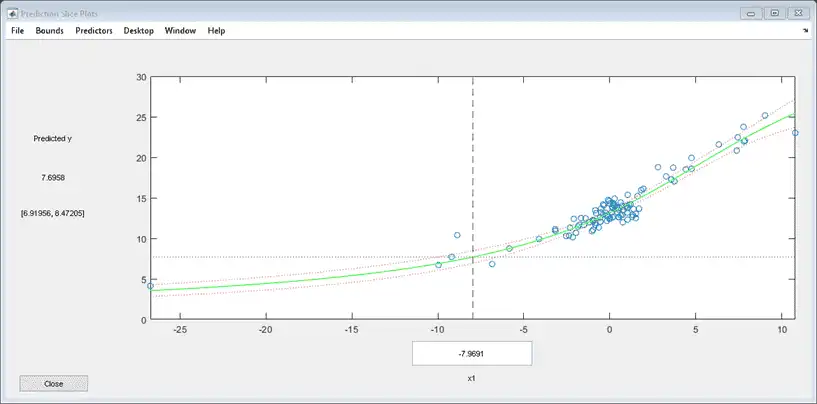
predict
The predict method predicts the mean responses and, if requested, gives confidence bounds. Find the predicted response values and predicted confidence intervals about the response at X values [-15;5;12].
Xnew = [-15;5;12]; [ynew,ynewci] = predict(mdl,Xnew)
ynew = 3×1
5.4122
18.9022
26.5161
ynewci = 3×2
4.8233 6.0010
18.4555 19.3490
25.0170 28.0151
The confidence intervals are reflected in the slice plot.
feval
The feval method predicts the mean responses. feval is often more convenient to use than predict when you construct a model from a dataset array.
Create the nonlinear model from a dataset array.
ds = dataset({X,'X'},{y,'y'});
mdl2 = fitnlm(ds,modelfun,beta0);
Find the predicted model responses (CDF) at X values [-15;5;12].
Xnew = [-15;5;12]; ynew = feval(mdl2,Xnew)
ynew = 3×1
5.4122
18.9022
26.5161
random
The random method simulates new random response values, equal to the mean prediction plus a random disturbance with the same variance as the training data.
Xnew = [-15;5;12]; ysim = random(mdl,Xnew)
ysim = 3×1
6.0505
19.0893
25.4647
Rerun the random method. The results change.
ysim = random(mdl,Xnew)
ysim = 3×1
6.3813
19.2157
26.6541