Support Vector Machines for Binary Classification 5

Create the Data Set

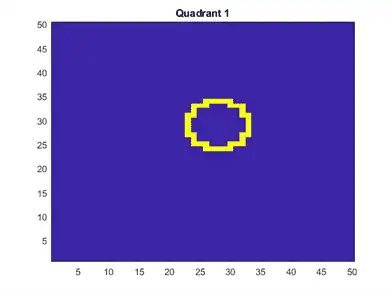
Randomly place a circle with radius five in a 50-by-50 image. Make 5000 images. Create a label for each image indicating the quadrant that the circle occupies. Quadrant 1 is in the upper right, quadrant 2 is in the upper left, quadrant 3 is in the lower left, and quadrant 4 is in the lower right. The predictors are the intensities of each pixel.

d = 50;  % Height and width of the images in pixels
n = 5e4; % Sample size

X = zeros(n,d^2); % Predictor matrix preallocation 
Y = zeros(n,1);   % Label preallocation
theta = 0:(1/d):(2*pi);
r = 5;            % Circle radius
rng(1);           % For reproducibility

for j = 1:n
    figmat = zeros(d);                       % Empty image
    c = datasample((r + 1):(d - r - 1),2);   % Random circle center
    x = r*cos(theta) + c(1);                 % Make the circle 
    y = r*sin(theta) + c(2);               
    idx = sub2ind([d d],round(y),round(x));  % Convert to linear indexing
    figmat(idx) = 1;                         % Draw the circle
    X(j,:) = figmat(:);                % Store the data
    Y(j) = (c(2) >= floor(d/2)) + 2*(c(2) < floor(d/2)) + ...
        (c(1) < floor(d/2)) + ...
        2*((c(1) >= floor(d/2)) & (c(2) < floor(d/2))); % Determine the quadrant
end

Plot an observation.

figure
imagesc(figmat)
h = gca;
h.YDir = 'normal';
title(sprintf('Quadrant %d',Y(end)))

Train the ECOC Model

Use a 25% holdout sample and specify the training and holdout sample indices.

p = 0.25;
CVP = cvpartition(Y,'Holdout',p); % Cross-validation data partition
isIdx = training(CVP);            % Training sample indices
oosIdx = test(CVP);               % Test sample indices

Create an SVM template that specifies storing the support vectors of the binary learners. Pass it and the training data to fitcecoc to train the model. Determine the training sample classification error.

t = templateSVM('SaveSupportVectors',true);
MdlSV = fitcecoc(X(isIdx,:),Y(isIdx),'Learners',t);
isLoss = resubLoss(MdlSV)

isLoss = 0

MdlSV is a trained ClassificationECOC multiclass model. It stores the training data and the support vectors of each binary learner. For large data sets, such as those in image analysis, the model can consume a lot of memory.

Determine the amount of disk space that the ECOC model consumes.

infoMdlSV = whos('MdlSV');
mbMdlSV = infoMdlSV.bytes/1.049e6

mbMdlSV = 763.6150

The model consumes 763.6 MB.

Improve Model Efficiency

You can assess out-of-sample performance. You can also assess whether the model has been overfit with a compacted model that does not contain the support vectors, their related parameters, and the training data.

Discard the support vectors and related parameters from the trained ECOC model. Then, discard the training data from the resulting model by using compact.

Mdl = discardSupportVectors(MdlSV);
CMdl = compact(Mdl);
info = whos('Mdl','CMdl');
[bytesCMdl,bytesMdl] = info.bytes;
memReduction = 1 - [bytesMdl bytesCMdl]/infoMdlSV.bytes

memReduction = 1×2

    0.0626    0.9996

In this case, discarding the support vectors reduces the memory consumption by about 6%. Compacting and discarding support vectors reduces the size by about 99.96%.

An alternative way to manage support vectors is to reduce their numbers during training by specifying a larger box constraint, such as 100. Though SVM models that use fewer support vectors are more desirable and consume less memory, increasing the value of the box constraint tends to increase the training time.

Remove MdlSV and Mdl from the workspace.

clear Mdl MdlSV

Assess Holdout Sample Performance

Calculate the classification error of the holdout sample. Plot a sample of the holdout sample predictions.

oosLoss = loss(CMdl,X(oosIdx,:),Y(oosIdx))

oosLoss = 0

yHat = predict(CMdl,X(oosIdx,:));
nVec = 1:size(X,1);
oosIdx = nVec(oosIdx);

figure;
for j = 1:9
    subplot(3,3,j)
    imagesc(reshape(X(oosIdx(j),:),[d d]))
    h = gca;
    h.YDir = 'normal';
    title(sprintf('Quadrant: %d',yHat(j)))
end
text(-1.33*d,4.5*d + 1,'Predictions','FontSize',17)

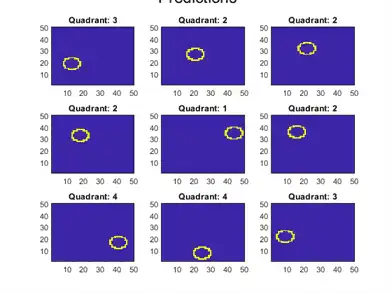
The model does not misclassify any holdout sample observations.