When you create surface plots using functions such as surf or mesh, you can customize the color scheme by calling the colormap function. If you want further control over the appearance, you can change the direction or pattern of the colors across the surface. This customization requires changing values in an array that controls the relationship between the surface and the colormap.
The CData property of a Surface object contains an indexing array C that associates specific locations in your plot with colors in the colormap. C has the following relationship to the surface z = f(x,y):
C is the same size as Z, where Z is the array containing the values of f(x,y) at each grid point on the surface.
The value at C(i,j) controls the color at the grid location (i,j) on the surface.
By default, C is equal to Z, which corresponds to colors varying with altitude.
By default, the range of C maps linearly to the number of rows in the colormap array.
For example, a 3-by-3 sampling of Z = X + Y has the following relationship to a colormap containing N entries.
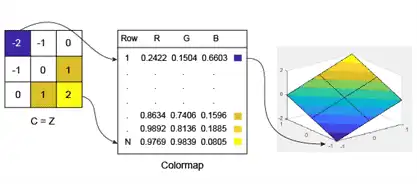
Notice that the smallest value (-2) maps to the first row in the colormap. The largest value (2) maps to the last row in the colormap. The intermediate values in C map linearly to the intermediate rows in the colormap.
The preceding surface plot shows how colors are assigned to vertices on the surface. However, the default behavior is to fill the patch faces with solid color. That solid color is based on the colors assigned to the surrounding vertices. For more information, see the FaceColor property description.
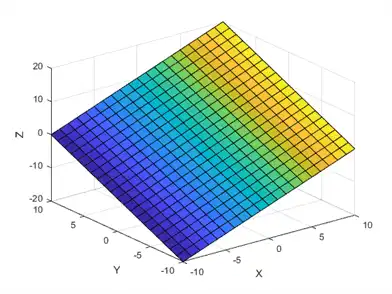
When using the default value of C=Z, the colors vary with changes in Z.
[X,Y] = meshgrid(-10:10);
Z = X + Y;
s = surf(X,Y,Z);
xlabel('X');
ylabel('Y');
zlabel('Z');
You can change this behavior by specifying C when you create the surface. For example, the colors on this surface vary with X.
C = X;
s = surf(X,Y,Z,C);
xlabel('X');
ylabel('Y');
zlabel('Z');
Alternatively, you can set the CData property directly. This command makes the colors vary with Y.
s.CData = Y;
The colors do not need to follow changes in a single dimension. In fact, CData can be any array that is the same size as Z. For example, the colors on this plane follow the shape of a sinc function.
R = sqrt(X.^2 + Y.^2) + eps; s.CData = sin(R)./(R);
Matlabsolutions.com provides guaranteed satisfaction with a commitment to complete the work within time. Combined with our meticulous work ethics and extensive domain experience, We are the ideal partner for all your homework/assignment needs. We pledge to provide 24*7 support to dissolve all your academic doubts. We are composed of 300+ esteemed Matlab and other experts who have been empanelled after extensive research and quality check.
Matlabsolutions.com provides undivided attention to each Matlab assignment order with a methodical approach to solution. Our network span is not restricted to US, UK and Australia rather extends to countries like Singapore, Canada and UAE. Our Matlab assignment help services include Image Processing Assignments, Electrical Engineering Assignments, Matlab homework help, Matlab Research Paper help, Matlab Simulink help. Get your work done at the best price in industry.
Desktop Basics - MATLAB & Simulink
Array Indexing - MATLAB & Simulink
Workspace Variables - MATLAB & Simulink
Text and Characters - MATLAB & Simulink
Calling Functions - MATLAB & Simulink
2-D and 3-D Plots - MATLAB & Simulink
Programming and Scripts - MATLAB & Simulink
Help and Documentation - MATLAB & Simulink
Creating, Concatenating, and Expanding Matrices - MATLAB & Simulink
Removing Rows or Columns from a Matrix
Reshaping and Rearranging Arrays
Add Title and Axis Labels to Chart
Change Color Scheme Using a Colormap
How Surface Plot Data Relates to a Colormap
How Image Data Relates to a Colormap
Time-Domain Response Data and Plots
Time-Domain Responses of Discrete-Time Model
Time-Domain Responses of MIMO Model
Time-Domain Responses of Multiple Models
Introduction: PID Controller Design
Introduction: Root Locus Controller Design
Introduction: Frequency Domain Methods for Controller Design
DC Motor Speed: PID Controller Design
DC Motor Position: PID Controller Design
Cruise Control: PID Controller Design
Suspension: Root Locus Controller Design
Aircraft Pitch: Root Locus Controller Design
Inverted Pendulum: Root Locus Controller Design
Get Started with Deep Network Designer
Create Simple Image Classification Network Using Deep Network Designer
Build Networks with Deep Network Designer
Classify Image Using GoogLeNet
Classify Webcam Images Using Deep Learning
Transfer Learning with Deep Network Designer
Train Deep Learning Network to Classify New Images
Deep Learning Processor Customization and IP Generation
Prototype Deep Learning Networks on FPGA
Deep Learning Processor Architecture
Deep Learning INT8 Quantization
Quantization of Deep Neural Networks
Custom Processor Configuration Workflow
Estimate Performance of Deep Learning Network by Using Custom Processor Configuration
Preprocess Images for Deep Learning
Preprocess Volumes for Deep Learning
Transfer Learning Using AlexNet
Time Series Forecasting Using Deep Learning
Create Simple Sequence Classification Network Using Deep Network Designer
Train Classification Models in Classification Learner App
Train Regression Models in Regression Learner App
Explore the Random Number Generation UI
Logistic regression create generalized linear regression model - MATLAB fitglm 2
Support Vector Machines for Binary Classification
Support Vector Machines for Binary Classification 2
Support Vector Machines for Binary Classification 3
Support Vector Machines for Binary Classification 4
Support Vector Machines for Binary Classification 5
Assess Neural Network Classifier Performance
Discriminant Analysis Classification
Train Generalized Additive Model for Binary Classification
Train Generalized Additive Model for Binary Classification 2
Classification Using Nearest Neighbors
Classification Using Nearest Neighbors 2
Classification Using Nearest Neighbors 3
Classification Using Nearest Neighbors 4
Classification Using Nearest Neighbors 5
Gaussian Process Regression Models
Gaussian Process Regression Models 2
Understanding Support Vector Machine Regression
Extract Voices from Music Signal
Align Signals with Different Start Times
Find a Signal in a Measurement
Extract Features of a Clock Signal
Filtering Data With Signal Processing Toolbox Software
Find Periodicity Using Frequency Analysis
Find and Track Ridges Using Reassigned Spectrogram
Classify ECG Signals Using Long Short-Term Memory Networks
Waveform Segmentation Using Deep Learning
Label Signal Attributes, Regions of Interest, and Points
Introduction to Streaming Signal Processing in MATLAB
Filter Frames of a Noisy Sine Wave Signal in MATLAB
Filter Frames of a Noisy Sine Wave Signal in Simulink
Lowpass Filter Design in MATLAB
Tunable Lowpass Filtering of Noisy Input in Simulink
Signal Processing Acceleration Through Code Generation
Signal Visualization and Measurements in MATLAB
Estimate the Power Spectrum in MATLAB
Design of Decimators and Interpolators
Multirate Filtering in MATLAB and Simulink
Australia
UK
UAE
Singapore
Canada
New
Zealand
Malaysia
USA
India
South Africa
Ireland
Saudi
Arab
Qatar
Kuwait
Hongkong
Copyright 2016-2023 www.matlabsolutions.com - All Rights Reserved.
Disclaimer : Any type of help and guidance service given by us is just for reference purpose. We never ask any of our clients to submit our solution guide as it is, anywhere.
