Abstract

fuzzy logic is increasingly used in decision-aided systems since it offers several advantages over other traditional decision-making techniques. The fuzzy decision support systems can easily deal with incomplete and/or imprecise knowledge applied to either linear or nonlinear problems. the implementation of a combination of a Real/Binary-Like coded Genetic Algorithm (RBLGA) and a Binary coded Genetic Algorithm (BGA) to automatically generate Fuzzy Knowledge Bases (FKB) from a set of numerical data. Both algorithms allow one to fulfill a contradictory paradigm in terms of FKB precision and simplicity (high precision generally translates into a higher level of complexity) considering a randomly generated population of potential FKBs. The RBLGA is divided into two principal coding methods: (1) a real coded genetic algorithm that maps the fuzzy sets repartition and number (which drives the number of fuzzy rules) into a set of real numbers and (2) a binary like coded genetic algorithm that deals with the fuzzy rule base relationships (a set of integers). The BGA deals with the entire FKB using a single bit string, which is called a genotype. The RBLGA uses three reproduction mechanisms, a BLX-α, a simple crossover and a fuzzy set reducer, while the BGA uses a simple crossover, a fuzzy set displacement mechanism and a rule reducer.

Introduction

Nowadays fuzzy logic is increasingly used in decision-aided systems since it offers several advantages over other traditional decision-making techniques. The fuzzy decision support systems (FDSS) can easily deal with incomplete and/or imprecise knowledge applied to either linear or nonlinear problems. In most cases decision making systems are used when there is:

an expert available to manually construct the FKB;
an important nonlinearity of the modeled process.

Hence, there is a difficulty to build a good enough mathematical model (impossible in some cases) that emulates the behavior of the problem to be solved. The construction of FKBs requires the evaluation of each potential solution (the generated FKBs), which allows to establish the accuracy level when comparing their behaviors (outputs) to the one in the learning data. The manual construction of an FKB requires the evaluation of each proposition made by the expert to measure its performance. If the result is not satisfactory, the expert determines the modifications either to the fuzzy sets repartition, to the fuzzy rule base or to both, in the hope of improving the accuracy.

Talk to Expert

Automatic generation of fuzzy knowledge bases using GAs

The automatic generation of fuzzy knowledge bases is performed using a GA. A GA is based on the analogy of the mechanics of natural genetics, and imitates the Darwinian survival-of-the-fittest approach (Baron, 1998). The GA uses four basic operations: crossover, mutation, evaluation and natural selection. Crossover and mutation are used respectively to generate and modify an FKB genotype and the natural selection sorts the different FKBs according to the performance criteria.

Learning process

The learning process is formulated as an optimization problem applied to the numerical data, using the BGA and the RBLGA in order to produce near to optimal FKBs.

An FKB contains the following entities/information:

the number of premises (inputs) and the number of conclusions (outputs);....
the number of fuzzy sets and their distribution on the premises and the conclusions; and....
the fuzzy rules (fuzzy rule base).....

Item 1 is a part of the problem's input data and all the features in items 2 and 3 are

Binary-Coded GA

Consider the following simple example minimizing the cost of a can∗.

Convert the following numbers to binary: d = 8, h = 10

Combine into one “chromosome”:

                    d = 01000, h = 01010
x = 0100001010

Single-point crossover:

Selected parents are not automatically eligible to cross-over process. The possibility to obtain offsprings from a pair of parents is determined by the cross-over probability. In general, the cross-over probability is chosen to be relatively high, in the order of 0.8 to 0.9 that means almost all parents will be replaced by their off-springs in the new generation. On the contrary, the probability of mutation to occur is relatively small, only 0.5% to 1% most of the times.

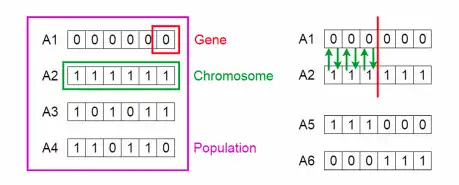Figure. Illustration of gene, chromosome and population (left) and mechanism resulting in off-spring with a single point cross-over (right) in a binary coded GA.