This section will provide a brief background on the k-Nearest Neighbors algorithm that we will implement in this tutorial and the Abalone dataset to which we will apply it.
The k-Nearest Neighbors algorithm or KNN for short is a very simple technique.
The entire training dataset is stored. When a prediction is required, the k-most similar records to a new record from the training dataset are then located. From these neighbors, a summarized prediction is made.
Similarity between records can be measured many different ways. A problem or data-specific method can be used. Generally, with tabular data, a good starting point is the Euclidean distance.
Once the neighbors are discovered, the summary prediction can be made by returning the most common outcome or taking the average. As such, KNN can be used for classification or regression problems.
There is no model to speak of other than holding the entire training dataset. Because no work is done until a prediction is required, KNN is often referred to as a lazy learning method.
In this tutorial we will use the Iris Flower Species Dataset.
The Iris Flower Dataset involves predicting the flower species given measurements of iris flowers.
It is a multiclass classification problem. The number of observations for each class is balanced. There are 150 observations with 4 input variables and 1 output variable. The variable names are as follows:
A sample of the first 5 rows is listed below.
5.1,3.5,1.4,0.2,Iris-setosa 4.9,3.0,1.4,0.2,Iris-setosa 4.7,3.2,1.3,0.2,Iris-setosa 4.6,3.1,1.5,0.2,Iris-setosa 5.0,3.6,1.4,0.2,Iris-setosa ...
The baseline performance on the problem is approximately 33%.
First we will develop each piece of the algorithm in this section, then we will tie all of the elements together into a working implementation applied to a real dataset in the next section.
This k-Nearest Neighbors tutorial is broken down into 3 parts:
These steps will teach you the fundamentals of implementing and applying the k-Nearest Neighbors algorithm for classification and regression predictive modeling problems.
Note: This tutorial assumes that you are using Python 3. If you need help installing Python, see this tutorial:
I believe the code in this tutorial will also work with Python 2.7 without any changes.
The first step is to calculate the distance between two rows in a dataset.
Rows of data are mostly made up of numbers and an easy way to calculate the distance between two rows or vectors of numbers is to draw a straight line. This makes sense in 2D or 3D and scales nicely to higher dimensions.
We can calculate the straight line distance between two vectors using the Euclidean distance measure. It is calculated as the square root of the sum of the squared differences between the two vectors.
Where x1 is the first row of data, x2 is the second row of data and i is the index to a specific column as we sum across all columns.
With Euclidean distance, the smaller the value, the more similar two records will be. A value of 0 means that there is no difference between two records.
Below is a function named euclidean_distance() that implements this in Python.
# calculate the Euclidean distance between two vectors def euclidean_distance(row1, row2): distance = 0.0 for i in range(len(row1)-1): distance += (row1[i] - row2[i])**2 return sqrt(distance)
You can see that the function assumes that the last column in each row is an output value which is ignored from the distance calculation.
We can test this distance function with a small contrived classification dataset. We will use this dataset a few times as we construct the elements needed for the KNN algorithm.
X1 X2 Y 2.7810836 2.550537003 0 1.465489372 2.362125076 0 3.396561688 4.400293529 0 1.38807019 1.850220317 0 3.06407232 3.005305973 0 7.627531214 2.759262235 1 5.332441248 2.088626775 1 6.922596716 1.77106367 1 8.675418651 -0.242068655 1 7.673756466 3.508563011 1
Below is a plot of the dataset using different colors to show the different classes for each point.
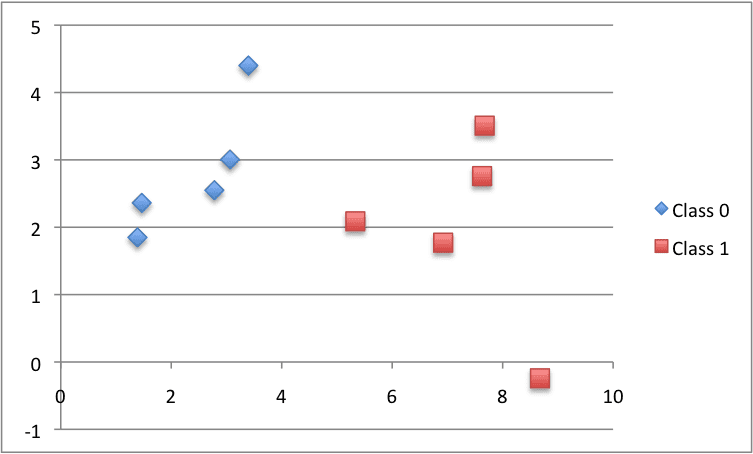
Putting this all together, we can write a small example to test our distance function by printing the distance between the first row and all other rows. We would expect the distance between the first row and itself to be 0, a good thing to look out for.
The full example is listed below.
# Example of calculating Euclidean distance from math import sqrt # calculate the Euclidean distance between two vectors def euclidean_distance(row1, row2): distance = 0.0 for i in range(len(row1)-1): distance += (row1[i] - row2[i])**2 return sqrt(distance) # Test distance function dataset = [[2.7810836,2.550537003,0], [1.465489372,2.362125076,0], [3.396561688,4.400293529,0], [1.38807019,1.850220317,0], [3.06407232,3.005305973,0], [7.627531214,2.759262235,1], [5.332441248,2.088626775,1], [6.922596716,1.77106367,1], [8.675418651,-0.242068655,1], [7.673756466,3.508563011,1]] row0 = dataset[0] for row in dataset: distance = euclidean_distance(row0, row) print(distance)
Running this example prints the distances between the first row and every row in the dataset, including itself.
0.0 1.3290173915275787 1.9494646655653247 1.5591439385540549 0.5356280721938492 4.850940186986411 2.592833759950511 4.214227042632867 6.522409988228337 4.985585382449795
Now it is time to use the distance calculation to locate neighbors within a dataset.
Neighbors for a new piece of data in the dataset are the k closest instances, as defined by our distance measure.
To locate the neighbors for a new piece of data within a dataset we must first calculate the distance between each record in the dataset to the new piece of data. We can do this using our distance function prepared above.
Once distances are calculated, we must sort all of the records in the training dataset by their distance to the new data. We can then select the top k to return as the most similar neighbors.
We can do this by keeping track of the distance for each record in the dataset as a tuple, sort the list of tuples by the distance (in descending order) and then retrieve the neighbors.
Below is a function named get_neighbors() that implements this.
# Locate the most similar neighbors def get_neighbors(train, test_row, num_neighbors): distances = list() for train_row in train: dist = euclidean_distance(test_row, train_row) distances.append((train_row, dist)) distances.sort(key=lambda tup: tup[1]) neighbors = list() for i in range(num_neighbors): neighbors.append(distances[i][0]) return neighbors
You can see that the euclidean_distance() function developed in the previous step is used to calculate the distance between each train_row and the new test_row.
The list of train_row and distance tuples is sorted where a custom key is used ensuring that the second item in the tuple (tup[1]) is used in the sorting operation.
Finally, a list of the num_neighbors most similar neighbors to test_row is returned.
We can test this function with the small contrived dataset prepared in the previous section.
The complete example is listed below.
# Example of getting neighbors for an instance from math import sqrt # calculate the Euclidean distance between two vectors def euclidean_distance(row1, row2): distance = 0.0 for i in range(len(row1)-1): distance += (row1[i] - row2[i])**2 return sqrt(distance) # Locate the most similar neighbors def get_neighbors(train, test_row, num_neighbors): distances = list() for train_row in train: dist = euclidean_distance(test_row, train_row) distances.append((train_row, dist)) distances.sort(key=lambda tup: tup[1]) neighbors = list() for i in range(num_neighbors): neighbors.append(distances[i][0]) return neighbors # Test distance function dataset = [[2.7810836,2.550537003,0], [1.465489372,2.362125076,0], [3.396561688,4.400293529,0], [1.38807019,1.850220317,0], [3.06407232,3.005305973,0], [7.627531214,2.759262235,1], [5.332441248,2.088626775,1], [6.922596716,1.77106367,1], [8.675418651,-0.242068655,1], [7.673756466,3.508563011,1]] neighbors = get_neighbors(dataset, dataset[0], 3) for neighbor in neighbors: print(neighbor)
Running this example prints the 3 most similar records in the dataset to the first record, in order of similarity.
As expected, the first record is the most similar to itself and is at the top of the list.
[2.7810836, 2.550537003, 0] [3.06407232, 3.005305973, 0] [1.465489372, 2.362125076, 0]
Now that we know how to get neighbors from the dataset, we can use them to make predictions.
The most similar neighbors collected from the training dataset can be used to make predictions.
In the case of classification, we can return the most represented class among the neighbors.
We can achieve this by performing the max() function on the list of output values from the neighbors. Given a list of class values observed in the neighbors, the max() function takes a set of unique class values and calls the count on the list of class values for each class value in the set.
Below is the function named predict_classification() that implements this.
# Make a classification prediction with neighbors def predict_classification(train, test_row, num_neighbors): neighbors = get_neighbors(train, test_row, num_neighbors) output_values = [row[-1] for row in neighbors] prediction = max(set(output_values), key=output_values.count) return prediction
We can test this function on the above contrived dataset.
Below is a complete example.
# Example of making predictions
from math import sqrt
# calculate the Euclidean distance between two vectors
def euclidean_distance(row1, row2):
distance = 0.0
for i in range(len(row1)-1):
distance += (row1[i] - row2[i])**2
return sqrt(distance)
# Locate the most similar neighbors
def get_neighbors(train, test_row, num_neighbors):
distances = list()
for train_row in train:
dist = euclidean_distance(test_row, train_row)
distances.append((train_row, dist))
distances.sort(key=lambda tup: tup[1])
neighbors = list()
for i in range(num_neighbors):
neighbors.append(distances[i][0])
return neighbors
# Make a classification prediction with neighbors
def predict_classification(train, test_row, num_neighbors):
neighbors = get_neighbors(train, test_row, num_neighbors)
output_values = [row[-1] for row in neighbors]
prediction = max(set(output_values), key=output_values.count)
return prediction
# Test distance function
dataset = [[2.7810836,2.550537003,0],
[1.465489372,2.362125076,0],
[3.396561688,4.400293529,0],
[1.38807019,1.850220317,0],
[3.06407232,3.005305973,0],
[7.627531214,2.759262235,1],
[5.332441248,2.088626775,1],
[6.922596716,1.77106367,1],
[8.675418651,-0.242068655,1],
[7.673756466,3.508563011,1]]
prediction = predict_classification(dataset, dataset[0], 3)
print('Expected %d, Got %d.' % (dataset[0][-1], prediction))
Running this example prints the expected classification of 0 and the actual classification predicted from the 3 most similar neighbors in the dataset.
Expected 0, Got 0.
We can imagine how the predict_classification() function can be changed to calculate the mean value of the outcome values.
We now have all of the pieces to make predictions with KNN. Let’s apply it to a real dataset.
This section applies the KNN algorithm to the Iris flowers dataset.
The first step is to load the dataset and convert the loaded data to numbers that we can use with the mean and standard deviation calculations. For this we will use the helper function load_csv() to load the file, str_column_to_float() to convert string numbers to floats and str_column_to_int() to convert the class column to integer values.
We will evaluate the algorithm using k-fold cross-validation with 5 folds. This means that 150/5=30 records will be in each fold. We will use the helper functions evaluate_algorithm() to evaluate the algorithm with cross-validation and accuracy_metric() to calculate the accuracy of predictions.
A new function named k_nearest_neighbors() was developed to manage the application of the KNN algorithm, first learning the statistics from a training dataset and using them to make predictions for a test dataset.
If you would like more help with the data loading functions used below, see the tutorial:
If you would like more help with the way the model is evaluated using cross validation, see the tutorial:
The complete example is listed below.
# k-nearest neighbors on the Iris Flowers Dataset
from random import seed
from random import randrange
from csv import reader
from math import sqrt
# Load a CSV file
def load_csv(filename):
dataset = list()
with open(filename, 'r') as file:
csv_reader = reader(file)
for row in csv_reader:
if not row:
continue
dataset.append(row)
return dataset
# Convert string column to float
def str_column_to_float(dataset, column):
for row in dataset:
row[column] = float(row[column].strip())
# Convert string column to integer
def str_column_to_int(dataset, column):
class_values = [row[column] for row in dataset]
unique = set(class_values)
lookup = dict()
for i, value in enumerate(unique):
lookup[value] = i
for row in dataset:
row[column] = lookup[row[column]]
return lookup
# Find the min and max values for each column
def dataset_minmax(dataset):
minmax = list()
for i in range(len(dataset[0])):
col_values = [row[i] for row in dataset]
value_min = min(col_values)
value_max = max(col_values)
minmax.append([value_min, value_max])
return minmax
# Rescale dataset columns to the range 0-1
def normalize_dataset(dataset, minmax):
for row in dataset:
for i in range(len(row)):
row[i] = (row[i] - minmax[i][0]) / (minmax[i][1] - minmax[i][0])
# Split a dataset into k folds
def cross_validation_split(dataset, n_folds):
dataset_split = list()
dataset_copy = list(dataset)
fold_size = int(len(dataset) / n_folds)
for _ in range(n_folds):
fold = list()
while len(fold) < fold_size:
index = randrange(len(dataset_copy))
fold.append(dataset_copy.pop(index))
dataset_split.append(fold)
return dataset_split
# Calculate accuracy percentage
def accuracy_metric(actual, predicted):
correct = 0
for i in range(len(actual)):
if actual[i] == predicted[i]:
correct += 1
return correct / float(len(actual)) * 100.0
# Evaluate an algorithm using a cross validation split
def evaluate_algorithm(dataset, algorithm, n_folds, *args):
folds = cross_validation_split(dataset, n_folds)
scores = list()
for fold in folds:
train_set = list(folds)
train_set.remove(fold)
train_set = sum(train_set, [])
test_set = list()
for row in fold:
row_copy = list(row)
test_set.append(row_copy)
row_copy[-1] = None
predicted = algorithm(train_set, test_set, *args)
actual = [row[-1] for row in fold]
accuracy = accuracy_metric(actual, predicted)
scores.append(accuracy)
return scores
# Calculate the Euclidean distance between two vectors
def euclidean_distance(row1, row2):
distance = 0.0
for i in range(len(row1)-1):
distance += (row1[i] - row2[i])**2
return sqrt(distance)
# Locate the most similar neighbors
def get_neighbors(train, test_row, num_neighbors):
distances = list()
for train_row in train:
dist = euclidean_distance(test_row, train_row)
distances.append((train_row, dist))
distances.sort(key=lambda tup: tup[1])
neighbors = list()
for i in range(num_neighbors):
neighbors.append(distances[i][0])
return neighbors
# Make a prediction with neighbors
def predict_classification(train, test_row, num_neighbors):
neighbors = get_neighbors(train, test_row, num_neighbors)
output_values = [row[-1] for row in neighbors]
prediction = max(set(output_values), key=output_values.count)
return prediction
# kNN Algorithm
def k_nearest_neighbors(train, test, num_neighbors):
predictions = list()
for row in test:
output = predict_classification(train, row, num_neighbors)
predictions.append(output)
return(predictions)
# Test the kNN on the Iris Flowers dataset
seed(1)
filename = 'iris.csv'
dataset = load_csv(filename)
for i in range(len(dataset[0])-1):
str_column_to_float(dataset, i)
# convert class column to integers
str_column_to_int(dataset, len(dataset[0])-1)
# evaluate algorithm
n_folds = 5
num_neighbors = 5
scores = evaluate_algorithm(dataset, k_nearest_neighbors, n_folds, num_neighbors)
print('Scores: %s' % scores)
print('Mean Accuracy: %.3f%%' % (sum(scores)/float(len(scores))))
Running the example prints the mean classification accuracy scores on each cross-validation fold as well as the mean accuracy score.
We can see that the mean accuracy of about 96.6% is dramatically better than the baseline accuracy of 33%.
Scores: [96.66666666666667, 96.66666666666667, 100.0, 90.0, 100.0] Mean Accuracy: 96.667%
We can use the training dataset to make predictions for new observations (rows of data).
This involves making a call to the predict_classification() function with a row representing our new observation to predict the class label.
... # predict the label label = predict_classification(dataset, row, num_neighbors)
We also might like to know the class label (string) for a prediction.
We can update the str_column_to_int() function to print the mapping of string class names to integers so we can interpret the prediction made by the model.
# Convert string column to integer
def str_column_to_int(dataset, column):
class_values = [row[column] for row in dataset]
unique = set(class_values)
lookup = dict()
for i, value in enumerate(unique):
lookup[value] = i
print('[%s] => %d' % (value, i))
for row in dataset:
row[column] = lookup[row[column]]
return lookup
Tying this together, a complete example of using KNN with the entire dataset and making a single prediction for a new observation is listed below.
# Make Predictions with k-nearest neighbors on the Iris Flowers Dataset
from csv import reader
from math import sqrt
# Load a CSV file
def load_csv(filename):
dataset = list()
with open(filename, 'r') as file:
csv_reader = reader(file)
for row in csv_reader:
if not row:
continue
dataset.append(row)
return dataset
# Convert string column to float
def str_column_to_float(dataset, column):
for row in dataset:
row[column] = float(row[column].strip())
# Convert string column to integer
def str_column_to_int(dataset, column):
class_values = [row[column] for row in dataset]
unique = set(class_values)
lookup = dict()
for i, value in enumerate(unique):
lookup[value] = i
print('[%s] => %d' % (value, i))
for row in dataset:
row[column] = lookup[row[column]]
return lookup
# Find the min and max values for each column
def dataset_minmax(dataset):
minmax = list()
for i in range(len(dataset[0])):
col_values = [row[i] for row in dataset]
value_min = min(col_values)
value_max = max(col_values)
minmax.append([value_min, value_max])
return minmax
# Rescale dataset columns to the range 0-1
def normalize_dataset(dataset, minmax):
for row in dataset:
for i in range(len(row)):
row[i] = (row[i] - minmax[i][0]) / (minmax[i][1] - minmax[i][0])
# Calculate the Euclidean distance between two vectors
def euclidean_distance(row1, row2):
distance = 0.0
for i in range(len(row1)-1):
distance += (row1[i] - row2[i])**2
return sqrt(distance)
# Locate the most similar neighbors
def get_neighbors(train, test_row, num_neighbors):
distances = list()
for train_row in train:
dist = euclidean_distance(test_row, train_row)
distances.append((train_row, dist))
distances.sort(key=lambda tup: tup[1])
neighbors = list()
for i in range(num_neighbors):
neighbors.append(distances[i][0])
return neighbors
# Make a prediction with neighbors
def predict_classification(train, test_row, num_neighbors):
neighbors = get_neighbors(train, test_row, num_neighbors)
output_values = [row[-1] for row in neighbors]
prediction = max(set(output_values), key=output_values.count)
return prediction
# Make a prediction with KNN on Iris Dataset
filename = 'iris.csv'
dataset = load_csv(filename)
for i in range(len(dataset[0])-1):
str_column_to_float(dataset, i)
# convert class column to integers
str_column_to_int(dataset, len(dataset[0])-1)
# define model parameter
num_neighbors = 5
# define a new record
row = [5.7,2.9,4.2,1.3]
# predict the label
label = predict_classification(dataset, row, num_neighbors)
print('Data=%s, Predicted: %s' % (row, label))
Running the data first summarizes the mapping of class labels to integers and then fits the model on the entire dataset.
Then a new observation is defined (in this case I took a row from the dataset), and a predicted label is calculated.
In this case our observation is predicted as belonging to class 1 which we know is “Iris-setosa“.
[Iris-virginica] => 0 [Iris-setosa] => 1 [Iris-versicolor] => 2 Data=[4.5, 2.3, 1.3, 0.3], Predicted: 1
This section lists extensions to the tutorial you may wish to consider to investigate.
Matlabsolutions.com provides guaranteed satisfaction with a
commitment to complete the work within time. Combined with our meticulous work ethics and extensive domain
experience, We are the ideal partner for all your homework/assignment needs. We pledge to provide 24*7 support
to dissolve all your academic doubts. We are composed of 300+ esteemed Matlab and other experts who have been
empanelled after extensive research and quality check.
Matlabsolutions.com provides undivided attention to each Matlab
assignment order with a methodical approach to solution. Our network span is not restricted to US, UK and Australia rather extends to countries like Singapore, Canada and UAE. Our Matlab assignment help services
include Image Processing Assignments, Electrical Engineering Assignments, Matlab homework help, Matlab Research Paper help, Matlab Simulink help. Get your work
done at the best price in industry.
Australia
UK
UAE
Singapore
Canada
New
Zealand
Malaysia
USA
India
South Africa
Ireland
Saudi
Arab
Qatar
Kuwait
Hongkong
Copyright 2016-2024 www.matlabsolutions.com - All Rights Reserved.
Disclaimer : Any type of help and guidance service given by us is just for reference purpose. We never ask any of our clients to submit our solution guide as it is, anywhere.
