How to Get Intermediate Signal of Block Diagram for Control System?


Hi, I have a block diagram (included below) of a control system for a mass damped cart and a PID control system. I have set up the system and solved for the output (X position), but am now looking to solve for the actual voltage applied to the system and cannot figure out how to get that data from MATLAB. Additionally here is my code that I currently have: % Cart Transfer Function s = tf('s'); G = 1.5531/(s^2+10.0938*s); G.u = 'V'; %input (voltage) G.y = 'X'; % ouput (x position) % PID Controller Transfer Function H = pid(120,10,40); H.u = 'e'; % input (error) H.y = 'V'; % output (voltage) % Combined Transfer Function for R to X (X/R) Sum = sumblk('e = R - X'); % solve for error in terms of R and X XR = connect(H,G,Sum,'R','X'); % Solve for step response [x1, t1] = step(XR,1.5); My attempted solution was as follows: % Combined Transfer Function for R to V (V/R) VR = connect(H,G,Sum,'R','V'); % [V, t2] = step(VR,1.5); % Commented out because it throws error: % Error using DynamicSystem/step % Cannot simulate the time response of improper (non-casual) models. However this results in an improper model (More zeros than poles). I feel like there should be a function in MATLAB, but I have spent hours searching and nothing seems to fit what I am looking for. Any help is greatly appreciated, and let me know if there is anything I forgot or anything I can clarify.
 Prashant Kumar answered .
2025-11-20
Prashant Kumar answered .
2025-11-20
s = tf('s');
G = 1.5531/(s^2+10.0938*s);
G.u = 'V'; %input (voltage)
G.y = 'X'; % ouput (x position)
% PID Controller Transfer Function
H = pid(120,10,40,1e-3)
H =
1 s
Kp + Ki * --- + Kd * --------
s Tf*s+1
with Kp = 120, Ki = 10, Kd = 40, Tf = 0.001
Continuous-time PIDF controller in parallel form.
H.u = 'e'; % input (error)
H.y = 'V'; % output (voltage)
% Combined Transfer Function for R to X (X/R)
Sum = sumblk('e = R - X'); % solve for e,rror in terms of R and X
%XR = connect(H,G,Sum,'R','X');
% Solve for step response
%[x1, t1] = step(XR,1.5);
% Combined Transfer Function for R to V and X
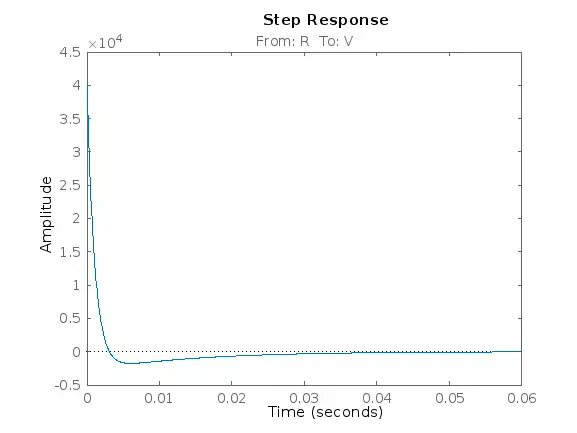
clsys = connect(H,G,Sum,'R',{'V' 'X'});
zpk(clsys)
ans =
From input "R" to output...
40120 s (s+0.08579) (s+2.905) (s+10.09)
V: -----------------------------------------
(s+0.08621) (s+2.584) (s+74.75) (s+932.7)
62310 (s+2.905) (s+0.08579)
X: -----------------------------------------
(s+0.08621) (s+2.584) (s+74.75) (s+932.7)
Continuous-time zero/pole/gain model.
% call step twice because the X repsonse takes longer than the V response
figure
step(clsys('X','R'))
figure
step(clsys('V','R'))