How to PID tuning to meet conditions for settling time and overshoot


PID tuning to meet conditions for settling time and overshoot while a stable system with minimum peak time and zero velocity error. So I am trying to find the gain values for a PI control system that would give me a settling time not exceeding 6 seconds, and an maximum overshoot not going over 5% while ensuring that the peaktime is the lowest it can be, and that the system is stable, and also has zero velocity error. I have written the following code. Starting with a kp and ki value of 1 each, I get a system that gives desirable overshoot and settling time, but I am wondering if the peaktime can be even lower while still having settling time <= 6 and overshoot <= 5. I am using the following toolboxes: Control System Toolbox Questions Using the rlocus function, I have also shown that the real parts of the poles are negative, so this demonstrates that my system is stable right? Also am I using Lsim correctly to determine if velocity error is zero? The resultant graph has a gray line showing the time response, and a blue line that is parallel to it. This means zero velocity error right? What is the best way to fine-tune the gain values kp and ki to minimize peak time while ensuring the above conditions are still met? I would like to use matlab only and no simulink for this please. clc clear all % plant transfer function G = tf([1], [0.5 1.5 1]) kp = 1 ki = 1 % PI controller C = tf([kp ki], [1 0]) % closed loop transfer function T = feedback(C*G, 1) rlocus(T) % Find the poles poles = pole(T) % step response figure; step(T); title('Step Response'); grid on; % Step analysis info = stepinfo(T) % Ramp Input t = 0:0.01:10; ramp = t; % System response to ramp figure; lsim(T, ramp, t); title('Ramp Response') legend grid on
 Prashant Kumar answered .
2025-11-20
Prashant Kumar answered .
2025-11-20
Here is the solution using pidtune(). There is no direct way to input the desired settling time and overshoot percentage; however, you can enter the desired phase margin. This has been a concern for me in MATLAB for many years. Nevertheless, based on the desired overshoot percentage, you can apply the formula from your lecture notes to determine the desired phase margin.
%% The Plant Gp = tf([1], [0.5 1.5 1])
Gp =
1
-------------------
0.5 s^2 + 1.5 s + 1
Continuous-time transfer function.
%% Using pidtune
Pm = 68.2; % desired Phase Margin
opt = pidtuneOptions('PhaseMargin', Pm, 'DesignFocus', 'balanced');
[Gc, info] = pidtune(Gp, 'pidf', opt)
Gc =
1 s
Kp + Ki * --- + Kd * --------
s Tf*s+1
with Kp = 2.02, Ki = 1.87, Kd = 0.489, Tf = 0.00619
Continuous-time PIDF controller in parallel form.
info = struct with fields:
Stable: 1
CrossoverFrequency: 1.4142
PhaseMargin: 72.6977
%% Closed-loop system Gcl = feedback(Gc*Gp, 1)
Gcl =
81.01 s^2 + 328.2 s + 302.2
-------------------------------------------------
0.5 s^4 + 82.31 s^3 + 324.4 s^2 + 489.8 s + 302.2
Continuous-time transfer function.
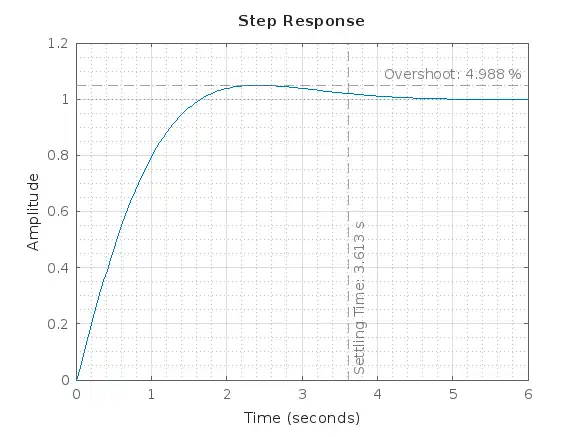
S = stepinfo(Gcl)
S = struct with fields:
RiseTime: 1.1479
TransientTime: 3.6131
SettlingTime: 3.6131
SettlingMin: 0.9088
SettlingMax: 1.0499
Overshoot: 4.9883
Undershoot: 0
Peak: 1.0499
PeakTime: 2.3938
step(Gcl), grid on, grid minor
xline(S.SettlingTime, '--', sprintf('Settling Time: %.3f s', S.SettlingTime), 'color', '#7F7F7F', 'LabelVerticalAlignment', 'bottom')
yline(1+S.Overshoot/100, '--', sprintf('Overshoot: %.3f %%', S.Overshoot), 'color', '#7F7F7F', 'LabelVerticalAlignment', 'top')