How to use fminunc for a 2D function composed of two functions?


I have: and I want to minimize it on the unit square I use the following code, close all; clear; clc;options = optimoptions(@fminunc,'Display','iter','Algorithm','quasi-newton');xy_guess = [0,0];[xy_opt,fval] = fminunc(@quadratic,xy_guess,options)function f = quadratic(in)x = in(1);y = in(2);f = -5.*x - 5.*y + 10.*x.^2 + 2.*x.*yf = 1/200.*(-1000.*x - 1000.*y + 400.*x.*y + 1200.*y.^2 + 5.*cos(30.*x) + 4.*cos(80.*x.^2) + 5.*cos(30.*y) + 4.*cos(80.*y^2)) But declaring f twice does not work. How should I declare this double-function as an input for fminunc ?
 Prashant Kumar answered .
2025-11-20
Prashant Kumar answered .
2025-11-20
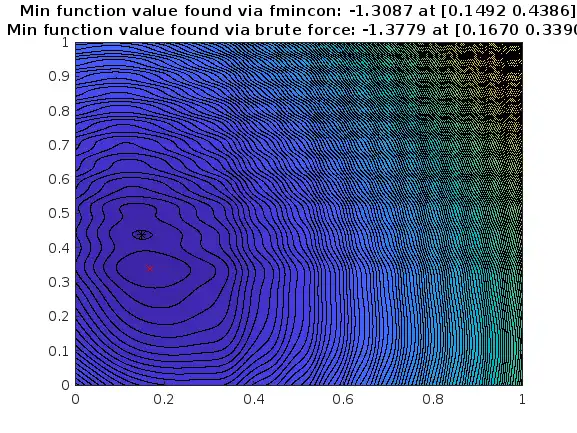
f = @(x) [x(1) x(2)]*[10 2;2 6]*[x(1);x(2)]-[5 5]*[x(1);x(2)]+(cos(30*x(1))+cos(30*x(2)))/40+(cos(80*x(1)^2)+cos(80*x(2)^2))/50; options = optimoptions(@fmincon); %options = optimoptions(@fmincon,'Display','iter','OptimalityTolerance',1e-12); lb = [0 0];% lower bounds ub = [1 1];% upper bounds x0 = [.5 .5]; % initial guess [xSol,fval,exitflag,output] = fmincon(f,x0,[],[],[],[],lb,ub,[],options); % solve optimization
Feasible point with lower objective function value found, but optimality criteria not satisfied. See output.bestfeasible.. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance.
% brute force searching the entire space for min function value x1 = 0:0.001:1; x2 = 0:0.001:1; [X1,X2] = meshgrid(x1,x2); fValBrute = arrayfun(@(x1,x2)f([x1 x2]),X1,X2); idxMin = find(fValBrute == min(fValBrute,[],'all')); % find minimum function value % plot contourf(X1,X2,fValBrute,150) hold on plot(xSol(1),xSol(2),'k*') % black star is the result of fmincon plot(X1(idxMin),X2(idxMin),'rx') % red x is the brute force result title({sprintf('Min function value found via fmincon: %.4f at [%.4f %.4f]',fval,xSol(1),xSol(2)); sprintf('Min function value found via brute force: %.4f at [%.4f %.4f]',fValBrute(idxMin),X1(idxMin),X2(idxMin))}) hold off