method for Numerical analysis


I know the classic method but i can not implement please help me.
 Prashant Kumar answered .
2025-11-20
Prashant Kumar answered .
2025-11-20
Here is a function I've created that hopefully answers your question:
function [x,fval,fevals] = NewtonFourier(f,ab,tol)
% NEWTONFOURIER Function that will efficiently find the local zero
% of an arbitrary function within a specified initial
% guess and tolerance.
%
% [x,fval,fevals] = NEWTONFOURIER(f,x0,tol);
%
% INPUT ARGUMENTS
% ================
% f Function handle to function to be searched
% ab Interval [a,b] in which root is assumed to be
% tol Desired relative error
%
% OUTPUT ARGUMENTS
% ================
% x The coordinate where f(x) = 0
% fval The evaluation of f(x)
% fevals Number of times the func was evaluated
% CHECK IF PROBLEM IS LIKELY UNSOLVABLE
if f(ab(1))*f(ab(2)) > 0
warning('f(a)f(b) > 0, there likely is no solution in [a,b].');
end
% DETERMINE APPROXIMATE DERIVATIVES OF func
fp = @(x) (f(x+tol)-f(x-tol))/(2*tol);
% INITIALIZE fevals
fevals = 2;
% INITIALIZE xn AND zn
xn = ab(2);
zn = ab(1);
% MAIN LOOP
err = Inf;
while err > tol
% Update root estimates
fxn = f(xn)/fp(xn);
xn = xn - fxn;
fzn = f(zn)/fp(zn);
zn = zn - fzn;
% Determine if converged
err = abs((fxn+fzn)/2);
% Update function evaluation counter
fevals = fevals+6;
end
% RETURN OUTPUTS
x = xn;
fval = f(xn);
fevals = fevals+1;
end
I've also written a demo file that solves the specific problem you've referenced in your question here:
% demo_NewtonFourier.m
% Initialize MATLAB
clear variables
close all
clc
% Define NewtonFourier.m Inputs
f = @(x) x.^3 + x.^2 + 1;
tol = 1e-6;
ab = [ -2 +2 ];
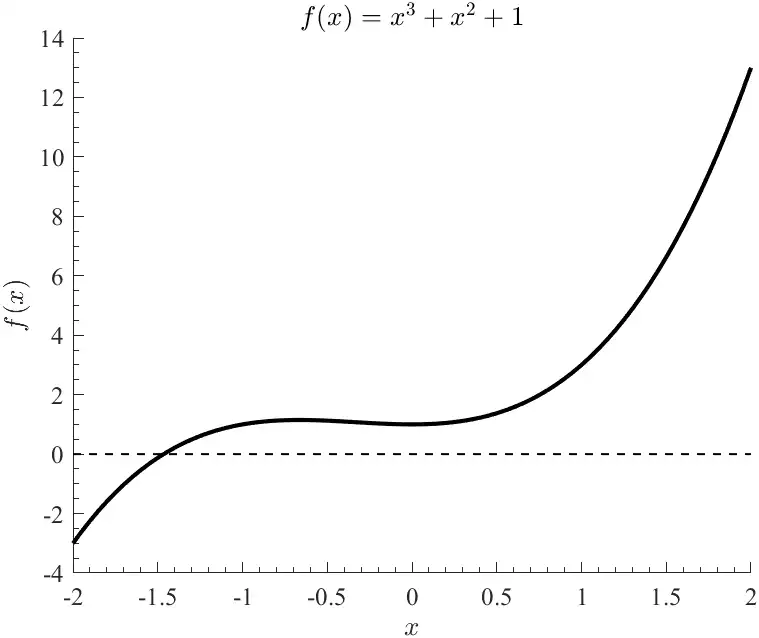
% Plot Function
x = ab(1) : 0.05 : ab(2);
y = f(x);
figure(1);
hold on
plot(x,y,'-k','LineWidth',2);
plot(x,0*x,'--k','LineWidth',1);
hold off
xlabel('$x$','Interpreter','latex');
ylabel('$f(x)$','Interpreter','latex');
title(['$ f(x) = ' latex(f(sym('x'))) '$'],'Interpreter','latex');
set(gca, 'FontSize', 12, 'FontName', 'Times', ...
'XMinorTick', 'on', 'YMinorTick', 'on', ...
'TickLength', [0.015, 0.0015]);
% Call NewtonFourier.m
[x,fval,fevals] = NewtonFourier(f,ab,tol)
The outputs of this demo file include the following figure showing the only real solution to be approximately -1.46,
x = -1.4656 fval = 4.4409e-16 fevals = 153
If you require explanation of the code snippets or need anything else, let me know!