Find the optimal value to maximize a function


Hi everyone..... could anyone help...... I need to find th optimal value of x0 and x1 to maximize R, where x1=d-x0..........the function MATLAB code: close all; clear all; clc; % System parameters F = 10000; % Number of files S = 100; % SBS cache capacity (set to 100) M = 50; % Cash capacity fraction alpha = 2; % Path loss exponent for LOS link c = 3e8; % Light speed fr = 1e12; % Operating frequency B = 10e6; % System bandwidth epsilon = 0.8; % Skewness factor K = 0.0016; % Molecular absorption coefficient P_M = 10^(64/10); % Transmit power MBS P_S = 10^(30/10); % Transmit power SBS sigma = 10^(-90/10); % Noise power N_L = 512; N_M = 16; eta = 1; x2 =30; % RIS-MBS distance d_range = 1:1:40; R = zeros(size(d_range)); for i = 1:length(d_range) d = d_range(i); sum1 = 0; for f = 1:F sum1 = sum1 + f^(-epsilon); end sum2 = 0; for f = 1:M sum2 = sum2 + f^(-epsilon)/sum1; end sum3 = 0; for f = (M + 1):(M + (S - M) / eta) sum3 = sum3 + (f^(-epsilon)) / sum1; end sum3 = sum3 * eta; beta = (c/(4*pi*fr))^2; % Spreading loss index Rs = B * log2(1 + (P_S * beta * (d-x1)^(-alpha) * exp(-K * (d-x1))) / sigma); Rm = B * log2(1 + (P_M * (N_L^2) * N_M * (beta * (d-x0)^(-alpha) * exp(-K * (d-x0))) * (beta * x2^(-alpha) * exp(-K * x2))) / sigma); Rt = Rs * (sum2 + sum3) + Rm * (1 - (sum2 + sum3)); R(i) = Rt; end figure plot(d_range, R, 'b^-') xlabel('SBS-RIS Distance, d') ylabel('Achievable Rate')
 John Williams answered .
2025-11-20
John Williams answered .
2025-11-20
close all; clear all; clc;
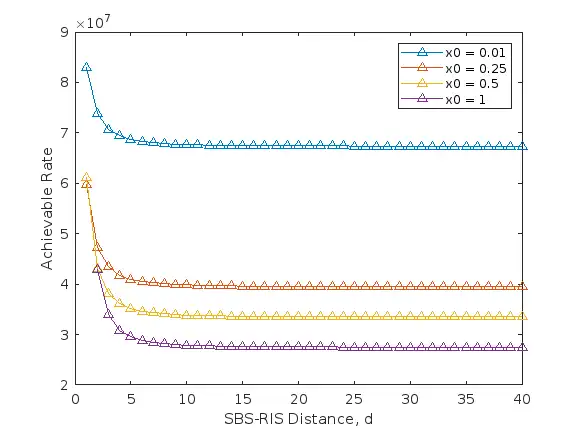
x0_range = [0.01 0.25 0.5 1];
% System parameters
F = 10000; % Number of files
S = 100; % SBS cache capacity (set to 100)
M = 50; % Cash capacity fraction
alpha = 2; % Path loss exponent for LOS link
c = 3e8; % Light speed
fr = 1e12; % Operating frequency
B = 10e6; % System bandwidth
epsilon = 0.8; % Skewness factor
K = 0.0016; % Molecular absorption coefficient
P_M = 10^(64/10); % Transmit power MBS
P_S = 10^(30/10); % Transmit power SBS
sigma = 10^(-90/10); % Noise power
N_L = 512;
N_M = 16;
eta = 1;
x2 =30; % RIS-MBS distance
d_range = 1:1:40;
R = zeros(numel(d_range),numel(x0_range));
for k = 1:numel(x0_range)
x0 = x0_range(k);
for i = 1:length(d_range)
d = d_range(i);
x1 = d-x0; % added line
% sum1 = 0;
% for f = 1:F
% sum1 = sum1 + f^(-epsilon);
% end
f = 1:F;
sum1 = sum(f.^(-epsilon));
% sum2 = 0;
% for f = 1:M
% sum2 = sum2 + f^(-epsilon)/sum1;
% end
f = 1:M;
sum2 = sum(f.^(-epsilon))/sum1;
% sum3 = 0;
% for f = (M + 1):(M + (S - M) / eta)
% sum3 = sum3 + (f^(-epsilon)) / sum1;
% end
% sum3 = sum3 * eta;
f = (M + 1):(M + (S - M) / eta);
sum3 = eta*sum(f.^(-epsilon))/sum1;
beta = (c/(4*pi*fr))^2; % Spreading loss index
Rs = B * log2(1 + (P_S * beta * (d-x1)^(-alpha) * exp(-K * (d-x1))) / sigma);
Rm = B * log2(1 + (P_M * (N_L^2) * N_M * (beta * (d-x0)^(-alpha) * exp(-K * (d-x0))) * (beta * x2^(-alpha) * exp(-K * x2))) / sigma);
Rt = Rs * (sum2 + sum3) + Rm * (1 - (sum2 + sum3));
R(i,k) = Rt;
leg{k} = ['x0 = ' num2str(x0)];
end
end
plot(d_range, R, '^-')
legend(leg)
xlabel('SBS-RIS Distance, d')
ylabel('Achievable Rate')