A multidimensional array in MATLAB® is an array with more than two dimensions. In a matrix, the two dimensions are represented by rows and columns.
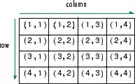
Each element is defined by two subscripts, the row index and the column index. Multidimensional arrays are an extension of 2-D matrices and use additional subscripts for indexing. A 3-D array, for example, uses three subscripts. The first two are just like a matrix, but the third dimension represents pages or sheets of elements.
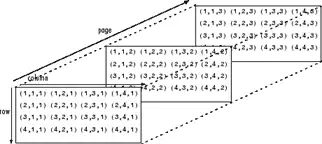
Creating Multidimensional Arrays
You can create a multidimensional array by creating a 2-D matrix first, and then extending it. For example, first define a 3-by-3 matrix as the first page in a 3-D array.
A = [1 2 3; 4 5 6; 7 8 9]
A = 3×3
1 2 3
4 5 6
7 8 9
Now add a second page. To do this, assign another 3-by-3 matrix to the index value 2 in the third dimension. The syntax A(:,:,2) uses a colon in the first and second dimensions to include all rows and all columns from the right-hand side of the assignment.
A(:,:,2) = [10 11 12; 13 14 15; 16 17 18]
A =
A(:,:,1) =
1 2 3
4 5 6
7 8 9
A(:,:,2) =
10 11 12
13 14 15
16 17 18
The cat function can be a useful tool for building multidimensional arrays. For example, create a new 3-D array B by concatenating A with a third page. The first argument indicates which dimension to concatenate along.
B = cat(3,A,[3 2 1; 0 9 8; 5 3 7])
B =
B(:,:,1) =
1 2 3
4 5 6
7 8 9
B(:,:,2) =
10 11 12
13 14 15
16 17 18
B(:,:,3) =
3 2 1
0 9 8
5 3 7
Another way to quickly expand a multidimensional array is by assigning a single element to an entire page. For example, add a fourth page to B that contains all zeros.
B(:,:,4) = 0
B =
B(:,:,1) =
1 2 3
4 5 6
7 8 9
B(:,:,2) =
10 11 12
13 14 15
16 17 18
B(:,:,3) =
3 2 1
0 9 8
5 3 7
B(:,:,4) =
0 0 0
0 0 0
0 0 0
Accessing Elements
To access elements in a multidimensional array, use integer subscripts just as you would for vectors and matrices. For example, find the 1,2,2 element of A, which is in the first row, second column, and second page of A.
A
A =
A(:,:,1) =
1 2 3
4 5 6
7 8 9
A(:,:,2) =
10 11 12
13 14 15
16 17 18
elA = A(1,2,2)
elA = 11
Use the index vector [1 3] in the second dimension to access only the first and last columns of each page of A.
C = A(:,[1 3],:)
C =
C(:,:,1) =
1 3
4 6
7 9
C(:,:,2) =
10 12
13 15
16 18
To find the second and third rows of each page, use the colon operator to create your index vector.
D = A(2:3,:,:)
D =
D(:,:,1) =
4 5 6
7 8 9
D(:,:,2) =
13 14 15
16 17 18
Manipulating Arrays
Elements of multidimensional arrays can be moved around in many ways, similar to vectors and matrices. reshape, permute, and squeeze are useful functions for rearranging elements. Consider a 3-D array with two pages.
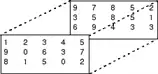
Reshaping a multidimensional array can be useful for performing certain operations or visualizing the data. Use the reshape function to rearrange the elements of the 3-D array into a 6-by-5 matrix.
A = [1 2 3 4 5; 9 0 6 3 7; 8 1 5 0 2]; A(:,:,2) = [9 7 8 5 2; 3 5 8 5 1; 6 9 4 3 3]; B = reshape(A,[6 5])
B = 6×5
1 3 5 7 5
9 6 7 5 5
8 5 2 9 3
2 4 9 8 2
0 3 3 8 1
1 0 6 4 3
reshape operates columnwise, creating the new matrix by taking consecutive elements down each column of A, starting with the first page then moving to the second page.
Permutations are used to rearrange the order of the dimensions of an array. Consider a 3-D array M.
M(:,:,1) = [1 2 3; 4 5 6; 7 8 9]; M(:,:,2) = [0 5 4; 2 7 6; 9 3 1]
M =
M(:,:,1) =
1 2 3
4 5 6
7 8 9
M(:,:,2) =
0 5 4
2 7 6
9 3 1
Use the permute function to interchange row and column subscripts on each page by specifying the order of dimensions in the second argument. The original rows of M are now columns, and the columns are now rows.
P1 = permute(M,[2 1 3])
P1 =
P1(:,:,1) =
1 4 7
2 5 8
3 6 9
P1(:,:,2) =
0 2 9
5 7 3
4 6 1
Similarly, interchange row and page subscripts of M.
P2 = permute(M,[3 2 1])
P2 =
P2(:,:,1) =
1 2 3
0 5 4
P2(:,:,2) =
4 5 6
2 7 6
P2(:,:,3) =
7 8 9
9 3 1
When working with multidimensional arrays, you might encounter one that has an unnecessary dimension of length 1. The squeeze function performs another type of manipulation that eliminates dimensions of length 1. For example, use the repmat function to create a 2-by-3-by-1-by-4 array whose elements are each 5, and whose third dimension has length 1.
A = repmat(5,[2 3 1 4])
A =
A(:,:,1,1) =
5 5 5
5 5 5
A(:,:,1,2) =
5 5 5
5 5 5
A(:,:,1,3) =
5 5 5
5 5 5
A(:,:,1,4) =
5 5 5
5 5 5
szA = size(A)
szA = 1×4
2 3 1 4
numdimsA = ndims(A)
numdimsA = 4
Use the squeeze function to remove the third dimension, resulting in a 3-D array.
B = squeeze(A)
B =
B(:,:,1) =
5 5 5
5 5 5
B(:,:,2) =
5 5 5
5 5 5
B(:,:,3) =
5 5 5
5 5 5
B(:,:,4) =
5 5 5
5 5 5
szB = size(B)
szB = 1×3
2 3 4
numdimsB = ndims(B)
numdimsB = 3